Hamilton Paths And Hamilton Circuit

 Definition (1):

A simple path in a graph G that passes through every vertex exactly once is called a Hamilton path .

Definition (2):

A simple circuit in a graph G that passes through every vertex exactly once is called a Hamilton circuit .

 Example (1):

G has Hamilton path: e, b, d, c, a .

And has a Hamilton circuit : e, b, d, c, a, e.

Observe that G has neither Euler path nor Euler circuit .

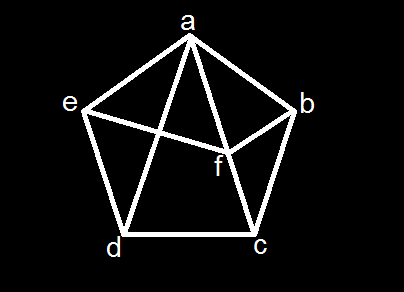
 Example (2):

The graph G has neither a Hamilton path nor a Hamilton circuit .

**There is no a specific role to know every graph G if it has a Hamilton path and Hamilton Circuit but we have some roles for some graphs. 

(1) A graph G with a vertex of degree one can not have a Hamilton circuit.

Ex:

b has deg=1 so G do not have Hamilton circuit.

(2) A graph with three vertices of degree one can not have a Hamilton path.

Ex:

a, b, and c have deg=1 so G do not have Hamilton path.

(3) (Dirac's Theorem) If G is a simple graph with n vertices (n >2) such that the degree of every vertex in G is at least n/2 , then G has a Hamilton circuit.

Ex:

The deg(any vertex) >2 Then G has Hamilton circuit.

(4) (ORE's Theorem) If G is a simple graph with n vertices (n >2) such that

 deg(u) + deg(v) >= n , for every pair of non-adjacent vertices u&v in G, then G has a Hamilton circuit.

Ex:

The deg(any vertex) + deg(any other vertex) >= 6 Then G has Hamilton circuit.