Definition (1):
A simple path in a graph G that passes through every vertex exactly once is called a Hamilton path .
Definition (2):
A simple circuit in a graph G that passes through every vertex exactly once is called a Hamilton circuit .
Example (1):
G has Hamilton path: e, b, d, c, a .
And has a Hamilton circuit : e, b, d, c, a, e.
Observe that G has neither Euler path nor Euler circuit .
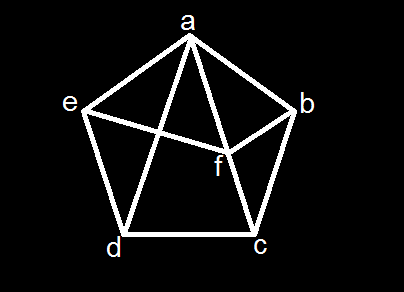
Example (2):
The graph G has neither a Hamilton path nor a Hamilton circuit .
**There is no a specific role to know every graph G if it has a Hamilton path and Hamilton Circuit but we have some roles for some graphs.
(1) A graph G with a vertex of degree one can not have a Hamilton circuit.
(2) A graph with three vertices of degree one can not have a Hamilton path.
(3) (Dirac's Theorem) If G is a simple graph with n vertices (n >2) such that the degree of every vertex in G is at least n/2 , then G has a Hamilton circuit.
(4) (ORE's Theorem) If G is a simple graph with n vertices (n >2) such that
deg(u) + deg(v) >= n , for every pair of non-adjacent vertices u&v in G, then G has a Hamilton circuit.
Ex:
The deg(any vertex) + deg(any other vertex) >= 6 Then G has Hamilton circuit.
Tags:
Combinatorial